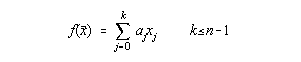
4. RAFINAREA MODELELOR CU MAI MULTI PARAMETRI
4.1. REGRESIA MULTIPLA SI POLINOMIALA
4.1.1. Regresia multipla
Fie setul de date experimentale y1,y2,...,yn care trebuie potrivit cu un model liniar de forma:
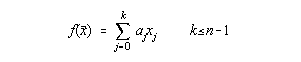
Functionala celor mai mici patrate are atunci forma:
![]()
sau:
![]()
Derivând dupa componenta m a vectorului ![]() , obtinem:
, obtinem:
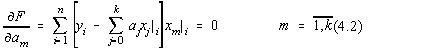
Acesta este un sistem liniar simetric de k+1 ecuatii cu k+1 necunoscute, care poate fi rescris sub forma:
![]()
Sau, inversând sumele, obtinem:
![]()
Observam ca matricea ![]() este
simetrica si cu determinant pozitiv, astfel încât sistemul liniar obtinut este normal.
Sistemul mai poate fi scris în forma:
este
simetrica si cu determinant pozitiv, astfel încât sistemul liniar obtinut este normal.
Sistemul mai poate fi scris în forma:
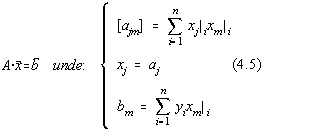
Din cauza coeficientului de corelatie matricea A este dominant diagonala.
Dezavantajul major al regresiei multiple consta în asa zisul numar de conditionare al matricii A.
Fie sistemul liniar:
![]()
în care matricile A si ![]() sunt
supuse unor perturbatii, reflectate în perturbatii ale lui
sunt
supuse unor perturbatii, reflectate în perturbatii ale lui ![]() [21], datorate influentei erorilor
experimentale în yi.
[21], datorate influentei erorilor
experimentale în yi.
![]()
Introducem numarul de conditionare ![]() si atunci:
si atunci:
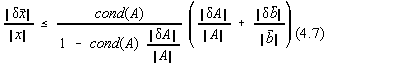
Pe de alta parte, cond(A) este supraunitar.
![]()
Cu cât numarul de conditionare este mai mare, cu atât matricea A este mai putin potrivita pentru calculul numeric. Spunem ca matricea A este rau conditionata.
Exemplu: Fie sistemul liniar:
![]()
cu solutia exacta
![]() .
.
Daca alegem b1=1,01 si b2=0,69, solutia obtinuta va fi x1'=-0,17
si x2'=0,22. Astfel, pentru erori de 1,4% în ![]() obtinem erori de 200% în solutie, deoarece cond(A)=300. Deoarece
sistemul nostru liniar este simetric, norma lui A este chiar valoarea proprie cea mai mare
în modul (vezi cap. V.).
obtinem erori de 200% în solutie, deoarece cond(A)=300. Deoarece
sistemul nostru liniar este simetric, norma lui A este chiar valoarea proprie cea mai mare
în modul (vezi cap. V.).
Patratul numarului de conditionare este egal cu raportul dintre modulele valorilor proprii cea mai mare si cea mai mica.
Astfel, precizia în determinarea solutiei sistemului liniar este data mai degraba de numarul de conditionare decât de valoarea determinantului.
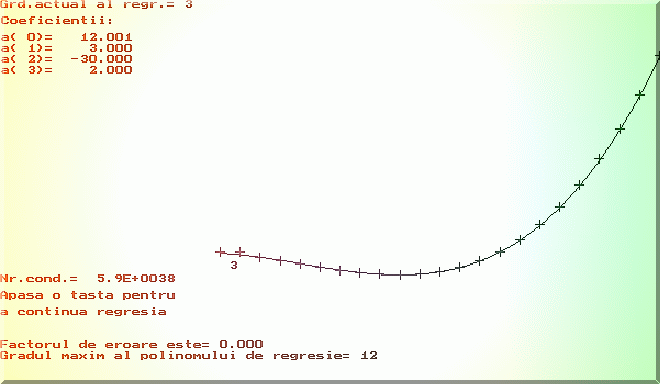
Fig. 4.1. Regresia polinomiala în absenta erorilor experimentale.
In cazul regresiei multiple, pentru matrici de ordin relativ mic (5-6),
solutionarea nu ridica probleme deosebite. Pentru valori mai mari, sistemul este rau
conditionat, adica det(A) este foarte mic iar ![]() are elemente foarte mari. De exemplu, pentru m=9, A-1 are elemente
de ordinul 10+12 iar erori de ordinul a 10-10 în yi
(masurat) conduc la erori de 300 în determinarea coeficientilor.
are elemente foarte mari. De exemplu, pentru m=9, A-1 are elemente
de ordinul 10+12 iar erori de ordinul a 10-10 în yi
(masurat) conduc la erori de 300 în determinarea coeficientilor.
În cazul unei necesitati imperioase a regresiei multiple, se calculeaza regresia
multipla pentru ordine crescatoare ale matricii A (dimensiunea vectorului ![]() ) pâna când nu se mai obtin progrese
semnificative în valoarea minimumului functionalei F. Acesta implica deci aplicarea
repetata a regresiei (Fig. 4.1. si 4.2.).
) pâna când nu se mai obtin progrese
semnificative în valoarea minimumului functionalei F. Acesta implica deci aplicarea
repetata a regresiei (Fig. 4.1. si 4.2.).
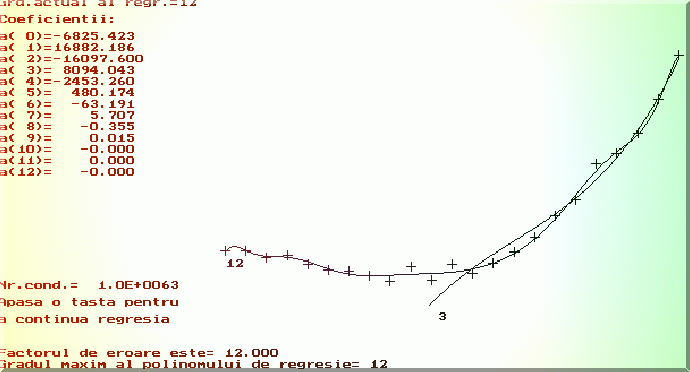
Fig. 4.2. Regresia polinomiala aplicata succesiv în prezenta erorilor experimentale.
Se observa ca în absenta erorilor experimentale, pentru un grad oricât de mare obtinem coeficientii polinomului test (Fig. 4.1.). In prezenta erorilor, primii coeficienti sunt foarte îndepartati de valorile adevarate.
4.1.2. Pseudosolutia unui sistem supradeterminat
Fie un sistem de n ecuatii cu m necunoscute, n>m, de forma:
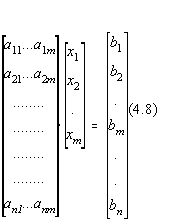
Problema poate fi solutionata în sensul celor mai mici patrate ca o problema de regresie multipla în care punem :
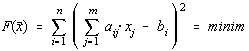
Sistemul normal asociat are forma simpla :
![]()
Din pacate, asemenea probleme au de obicei o matrice rau conditionata. Un exemplu, [21]:
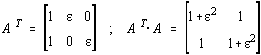
pentru care ![]() si tinde
catre Ą pentru e ® 0.
si tinde
catre Ą pentru e ® 0.
4.1.3. Regresia polinomiala
În cazul regresiei polinomiale, forma ecuatiilor sistemului normal (simetric si cu matrice pozitiv definita) este :
![]()
pentru ecuatia m.
Pentru cazul regresiei patratice (polinom de gradul 2) sunt utile formulele:
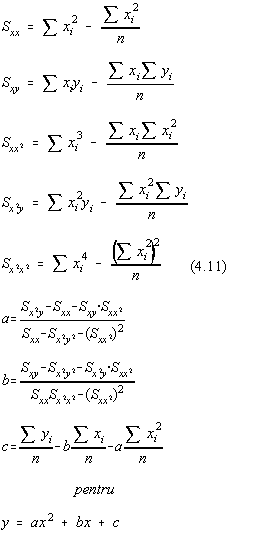
In cazul regresiei polinomiale se mai poate calcula simplu si coeficientul de corelatie între variabilele x si y, care sunt considerate independente :
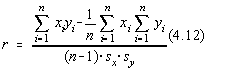
Se observa ca dintre variabilele xj doar variabila x1=x
este considerata aleatoare, deci coeficientul de corelatie calculat are sens doar pentru
regresia liniara. Pentru regresia multipla propriu zisa trebuie sa calculam coeficientii
de corelatie ![]() si sa discutam
corelatia în termenii distributiei normale multidimensionale.
si sa discutam
corelatia în termenii distributiei normale multidimensionale.
Este o greseala ca prin cresterea gradului regresiei polinomiale sa obtinem o garantata crestere a coeficientului de corelatie si pe acesta baza sa sustinem ca modelul polinomial obtinut este adecvat din punct de vedere fizic.
Sa aratam ca daca variabila x este distribuita normal, variabila y=x2 nu este obligatoriu distribuita normal în jurul mediei [16].
Fie Q functia de distributie a erorilor pentru variabila aleatoare y, iar P functia de distributie normala a erorilor pentru variabila aleatoare x:
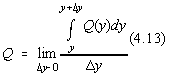
Deoarece:
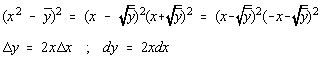
integrând prin parti obtinem:
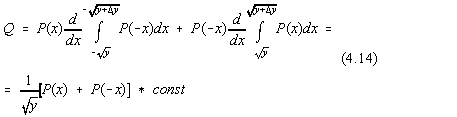
Deci distributia Q este normala doar daca ![]() .
.
Aceasta deducere ne arata ca în cazul regresiei polinomiale presupunerea x2=x2, x3=x3, x4=x4, s.a.m.d. implica de fapt ortogonalitatea variabilelor x1, x2,...,xn în sensul probabilist, deci baza x, x2, x3 este ortogonala, ipoteza valabila de obicei pentru polinoamele trigonometrice. Presupunerea ca erorile de esantionare în x2, x3,...,xk urmeaza o distributie normala este implicita dar nu este de obicei demonstrata. De aceea avem nevoie de o baza fizica solida a modelului. In mod asemanator, putem propune cu usurinta pentru variabilele xi forme ca:
![]()
Modelele pur polinomiale sunt rare în fizica. Dupa cum am aratat, este nevoie ca
![]() pentru ca polinoamele xn
sa fie considerate independente.
pentru ca polinoamele xn
sa fie considerate independente.
De exemplu în cazul comportarii din Fig.4.3. este sugerata o evolutie a unui experiment care consta din competitia a doua modele fizice neliniare si pentru care este recomandata analiza separata pe cele doua domenii.
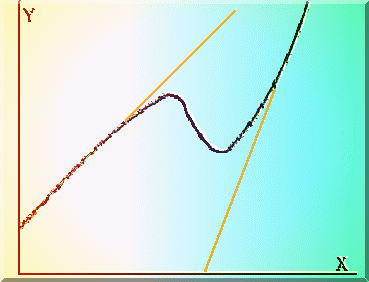
Fig. 4.3. Competitia a doua modele fizice cuasiliniare, care nu trebuie tratata prin regresie polinomiala.
În programele exemplificative se poate evidentia efectul erorilor experimentale asupra determinarii parametrilor modelului multiliniar. Fig.4.1. si Fig.4.2. prezinta rezultatul tipic în regresia polinomiala, în absenta, respectiv în prezenta erorilor experimentale .
4.2. AJUSTAREA PARAMETRILOR MODELELOR FIZICE NELINIARE
4.2.1. Cazul test pentru metodele de rezolvare a problemei celor mai mici patrate cu modele neliniare
Cazul test propus provine dintr-un experiment de urmarire a cresterii grauntilor în oxidul mixt (U,Th)O2. Înainte de a trece la discutarea metodelor care pot fi folosite pentru modelarea experimentului, trebuie sa precizam ca nici o metoda pentru rezolvarea problemei celor mai mici patrate pentru modelele neliniare (numita si "fitare") nu functioneaza "direct", ci are nevoie de valori initiale cât mai apropiate de realitate iar erorile experimentale trebuie sa fie bine caracterizate si acceptabil de mici, astfel încât modelul sa poata fi determinat univoc.
Nr. crt.(I) |
D(I) (Microni) |
T(I) (Ore) |
| 1 | 12,0 | 0 |
| 2 | 15,7 | 10 |
| 3 | 18,8 | 30 |
| 4 | 20,2 | 100 |
| 5 | 19,2 | 300 |
Modelul este:
![]()
![]()
cu rezultatele finale: x(1)=19,73; x(2)=0,393; x(3)=0,06767, pornind cu valorile initiale (tipice): x(1)=20; x(2)=0,5;x(3)=0,3. De observat ca în experimentul citat, se admite o eroare de 2 microni pentru masuratorile individuale, adica Fminim=20, însa desigur aceasta nu ne asigura de calitatea modelarii.
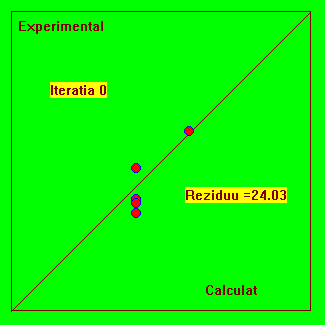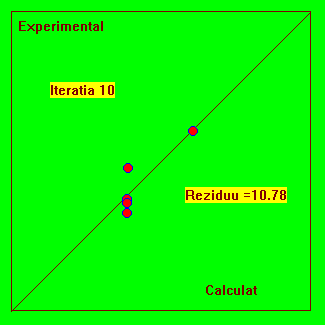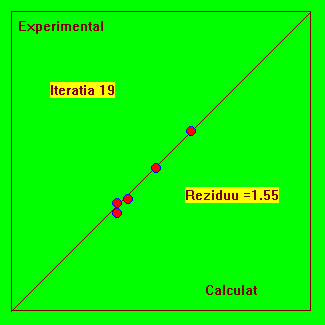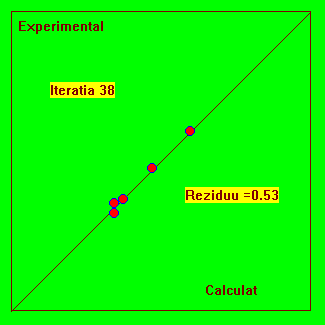
Fig. 4.4 Reprezentarea experimental-calculat pentru urmarirea evolutiei procesului iterativ.
Acest model are o asimptota si o functie tipic dificila pentru fitare, deoarece ea solicita limitele de reprezentare ale calculatorului pentru valori rau alese ale parametrilor si deci nu riscam vicii ascunse. Indiferent câti parametrii ar avea modelul, putem face reprezentarea din Fig. 4.4. Daca modelul teoretic este bine ajustat (fitat) atunci punctele trebuie sa se situeze pe prima bisectoare.
De asemenea, mai multe experimente fitate cu aceleasi model, trebuie sa situeze pe aceeasi prima bisectoare.
Eficienta unor metode de minimizare pentru modele neliniare poate fi urmarita în Fig.4.5. Se observa ca eficienta fitarii este cu atât mai buna cu cât metoda folosita este mai complexa. Cea mai simpla clasificare raspunde cerintei de calcul al derivatelor, care ar trebui tipic calculate analitic si deci s-ar putea induce erori grosolane în rezolvarea problemei, deoarece functionala celor mai mici patrate este de obicei complicat de derivat.
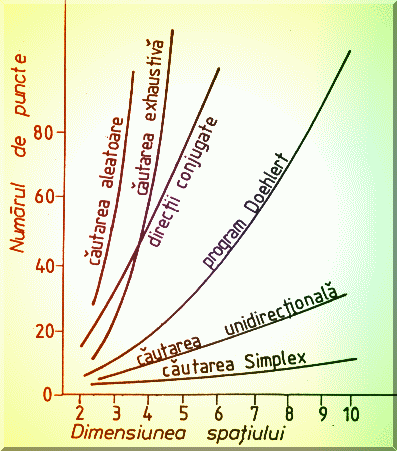
Fig. 4.5. Comparatia diferitelor metode de cautare a minimului pentru modele neliniare, fara calculul derivatelor partiale, dupa [25].
4.2.2. Ajustarea pasului si criterii de oprire în metodele de minimizare
Fie procesul iterativ:
![]()
Sa scriem acum:
![]()
în sensul ca procesul iterativ are o anumita evolutie în timp.
Aceasta evolutie nu poate fi prescrisa si de aceea:
![]()
permite modificarea pasului în procesele iterative, iar D t poate fi modificat.
Ajustarea pasului în procesul iterativ, astfel încât sa permita o apropiere cât mai
rapida de solutie se numeste stationarizare. Într-o analogie fizica, scaderea
pasului are un echivalent în rostogolirea unei bile pe o suprafata de ecuatie ![]() pâna se ajunge într-o groapa, adica
într-un punct stationar (Fig.4.6.) cu aparitia a doua forte de frecare: de tip Stokes
(proportionala cu viteza) si cealalta proportionala cu normala la suprafata. Daca nu se
ajunge în punctul stationar, spunem ca avem o metoda disipativa [7].
pâna se ajunge într-o groapa, adica
într-un punct stationar (Fig.4.6.) cu aparitia a doua forte de frecare: de tip Stokes
(proportionala cu viteza) si cealalta proportionala cu normala la suprafata. Daca nu se
ajunge în punctul stationar, spunem ca avem o metoda disipativa [7].
În apropierea punctelor stationare, avem un echilibru de forte de forma:
![]()
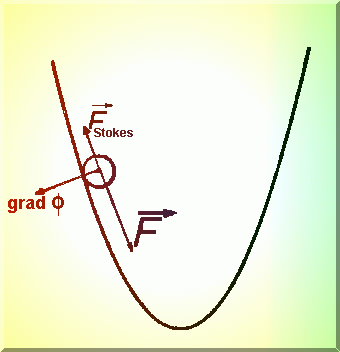
Fig.4.6. Modelul fizic pentru ajustarea pasului.
unde g >0 este coeficientul de frecare de tip Stokes, iar gradF da o forta de frecare proportionala cu normala la suprafata.
Pentru fixarea ideilor, sa punem:
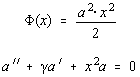
cu ecuatia caracteristica:
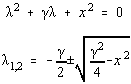
si solutia generala:
a=c1exp(l 1t)+c2exp(l 2t)
pentru l 1ą l 2 , adica g ą 2x. Astfel, descresterea în pasul iterativ depinde de forma suprafetei analizate (Fig.4.7.)
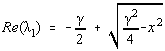
1 Daca g << 2x solutia problemei tinde încet catre pozitia de echilibru, oscilând în jurul ei (din cauza exponentialelor de argument imaginar).
2 Daca g >> 2x evolutia este de asemenea lenta. Analogia fizica ne indica o evolutie lenta catre minim daca coeficientul de frecare este prea mare.
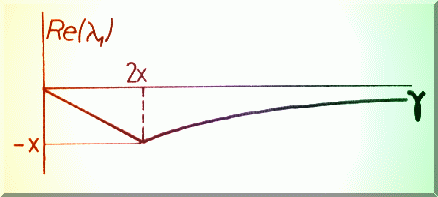
Fig. 4.7. Solutia ecuatiei. diferentiale la ajustarea pasului.
Deci, în general valoarea optima a lui este situata undeva între cele doua cazuri si depinde de forma suprafetei pe care se face cautarea. În cazul functionalei celor mai mici patrate, pentru a preveni o evolutie divergenta a procesului iterativ în vecinatatea solutiei, trebuie sa testam la fiecare iteratie:
- obtinerea unui anumit numar de cifre semnificative pentru toti parametrii sau o apropiere semnificativa de solutie, caz în care s-ar putea sa trebuiasca micsorate corectiile aj. Micsorarea corectiilor se mai numeste si ajustarea pasului. Maniera de ajustare a pasului este specifica fiecarei metode numerice iterative. Prezentam în continuare cazul în care pot fi folosite derivatele partiale de ordinul II, caz specific metodei Gauss-Newton.
Pentru aceasta, sa dezvoltam în serie ![]() dupa corectiile D a. Dupa primele k iteratii
obtinem [30]:
dupa corectiile D a. Dupa primele k iteratii
obtinem [30]:
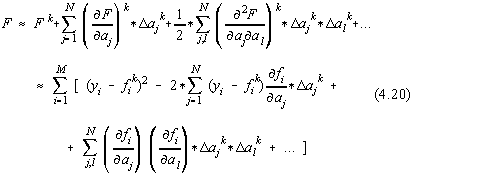
Sa consideram pentru micsorarea corectiilor un factor astfel încât: ![]() ,
, ![]() . Atunci, relatia anterioara poate fi scrisa în forma:
. Atunci, relatia anterioara poate fi scrisa în forma:
![]()
care descrie o parabola cu minimul în proximitatea solutiei.
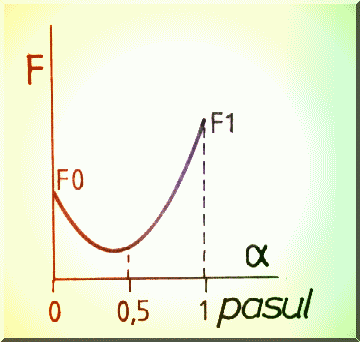
Fig. 4.8. Ajustarea pasului pentru metoda celor mai mici patrate.
În acel punct obtinem:
![]()
Astfel, în proximitatea solutiei (a =0) este permisa cautarea de-a lungul gradientului, fara calculul derivatelor de ordin superior.
Strategia de ajustare a pasului consta în micsorarea lui a în cazul în care pentru a =1 se obtine divergenta, sau schimbarea semnului corectiilor, denumita "cautare ineficienta".
Ajustarea lungimii pasului se poate face pornind de la polinomul de interpolare Lagrange de ordinul 2 care trece prin punctele a = 0 (vechea iteratie), a =0.5 si a =1 (noua iteratie-care este divergenta) cu valorile functionalei respectiv : F0, F0.5, F2 (Fig. 4.8). Pentru pasul h=0.5, derivatele polinomului Lagrange sunt:
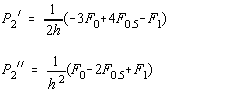
si furnizeaza minimul parabolei ca P2"/P2':
![]()
Criteriile de oprire pot fi de doua feluri :
![]() Terminatia anormala, datorata cautarii
ineficiente. Daca algoritmul ales nu dispune de un criteriu obiectiv pentru stabilirea
eficientei cautarii, în mod obisnuit se limiteaza numarul de evaluari ale functionalei
celor mai mici patrate.
Terminatia anormala, datorata cautarii
ineficiente. Daca algoritmul ales nu dispune de un criteriu obiectiv pentru stabilirea
eficientei cautarii, în mod obisnuit se limiteaza numarul de evaluari ale functionalei
celor mai mici patrate.
![]() Terminatia normala, atunci când
parametrii modelului au fost obtinuti cu precizia dorita. Tipic, aceasta înseamna ca la
doua iteratii succesive toti parametrii modelului coincid cu un numar prescris de cifre
semnificative. Desigur, pentru valori initiale rau alese ale parametrilor, acesta nu ne
asigura ca valoarea minimului functionalei celor mai mici patrate a fost bine gasita.
Terminatia normala, atunci când
parametrii modelului au fost obtinuti cu precizia dorita. Tipic, aceasta înseamna ca la
doua iteratii succesive toti parametrii modelului coincid cu un numar prescris de cifre
semnificative. Desigur, pentru valori initiale rau alese ale parametrilor, acesta nu ne
asigura ca valoarea minimului functionalei celor mai mici patrate a fost bine gasita.
4.2.3. Metode care nu necesita evaluarea derivatelor
4.2.3.1. Metoda cautarii exhaustive si cautarea aleatoare
Cele mai simple metode de cautare a minimului sunt:
a). Metoda cautarii exhaustive, în care pentru parametrii modelului se propun anumite domenii de variatie si se cauta întru-un ciclu valoarea cea mai convenabila, de exemplu, pentru cazul test:
18 Ł x(1) Ł 22 cu pasul 0,001
0 Ł x(2) Ł 1 cu pasul 0,001
0 Ł x(3) Ł 1 cu pasul 0,001.
b). Metoda cautarii aleatoare (nedeterminista) care utilizeaza generatorul de numere aleatoare al calculatorului ( de exemplu RND în limbajul BASIC) pentru a acoperi acelasi domeniu de cautare ca mai sus, retinându-se valoarea cea mai convenabila, adica aceea care da cea mai mica valoare pentru functionala celor mai mici patrate:
x(1)=20+(RND-0,5)*4
x(2)=0,5+(RND-0,5)*1
x(3)=0,5+(RND-0,5)*1
Aceasta metoda nu are un criteriu de oprire.
De observat ca aceste metode sunt utile mai ales atunci când avem doar o idee vaga despre valorile initiale ale parametrilor care trebuie livrati metodelor deterministe.
4.2.3.2. Cautarea Simplex (algoritmul Nelder si Mead)
Algoritmul nu necesita evaluarea derivatelor functionalei celor mai mici patrate si pleaca de la observatia lui Kantorovici ca pentru o problema de optimizare cu doua variabile, o dreapta oarecare în planul x1,x2 delimiteaza un semispatiu în care se afla optimul (Fig. 4.9).
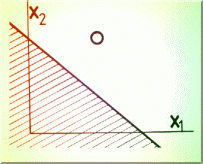
Fig. 4.9.
Localizarea (delimitarea) optimului se poate face atunci cu ajutorul a 3 drepte care construiesc un triunghi (Fig. 4.10.), pe care îl numim SIMPLEX. Deci pentru un spatiu cu N dimensiuni, simplexul va avea N+1 vârfuri.
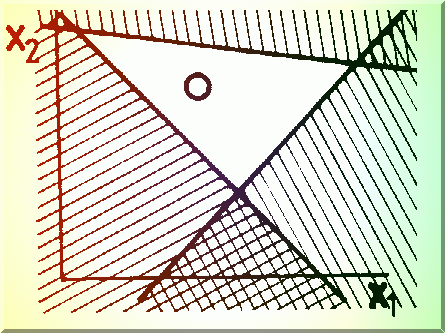
Fig. 4.10. Localizarea optimului într-un plan.
In cautarea SIMPLEX bidimensionala (Fig. 4.11.), se construiesc triunghiuri si se compara valorile functiei în vârfurile simplexului. Vârful cu valoarea cea mai defavorabila este îndepartata si se construieste un nou vârf, simetricul sau fata de linia celorlalte doua vârfuri.
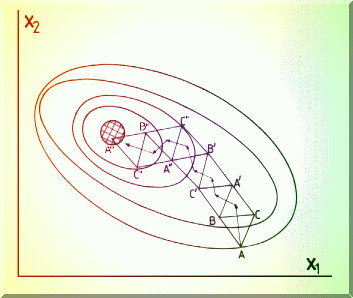
Fig. 4.11.. Principiul cautarii Simplex a minimului într-un spatiu bidimensional.
Construirea unui punct simetric tine cont de ponderea egala a variabilelor în plan, Fig. 4.12., si atunci se face relativ la mediatoarea segmentului AB de forma:
![]()
ceea ce corespunde evident centrului de greutate al segmentului AB.
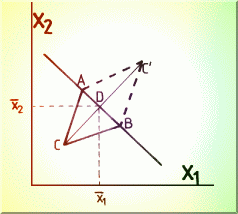
Fig. 4.12.
Coordonatele vârfului simetric fata de vârful cel mai defavorabil C pot fi obtinute
folosind ![]() si
si ![]() (Fig. 4.13),
(Fig. 4.13), ![]() . Linia AB este o
"oglinda", punctul C fiind cel mai dezavantajos din simplexul ABC.
. Linia AB este o
"oglinda", punctul C fiind cel mai dezavantajos din simplexul ABC.
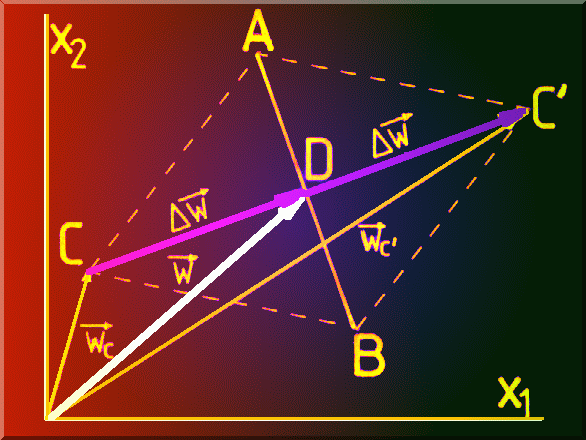
Fig. 4.13. Descrierea vectoriala constructiei pentru cautarea Simplex.
Se construieste un nou simplex ABC' în care se va cauta din nou punctul cel mai
defavorabil. Pentru o cautare cât mai eficienta, se pot propune pentru noul vârf mai
multe pozitii de pe aceeasi mediatoare, de exemplu ![]() unde poate lua mai multe valori, de exemplu (Fig.
4.14.): g = 0,5 pentru restrângeri (reveniri în semiplanul
vechi); g = 0,5 pentru contractii; g
= 1 pentru simplex obisnuit si g = 2 pentru expansiune.
unde poate lua mai multe valori, de exemplu (Fig.
4.14.): g = 0,5 pentru restrângeri (reveniri în semiplanul
vechi); g = 0,5 pentru contractii; g
= 1 pentru simplex obisnuit si g = 2 pentru expansiune.
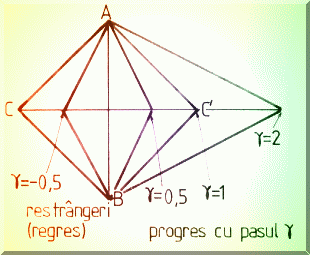
Fig. 4.14. Ajustarea pasului în cautarea Simplex.
Prin generalizare, într-un spatiu cu N dimensiuni, coordonatele punctului de oglindire
![]() pentru construirea noului simplex
se pot calcula cu formula:
pentru construirea noului simplex
se pot calcula cu formula:
![]()
în care consideram ca a fost eliminat vârful i.
Criteriul de oprire cel mai natural pentru acest algoritm este dat de ideea initiala a lui Kantorovici ca dreapta împarte planul în doua semiplane, favorabil si defavorabil. Deci, daca în cursul cautarii trebuie sa ne întoarcem în zona defavorabila de 1,65*N ori atunci cautarea este ineficienta, iar executia este oprita [25].
O generalizare a algoritmului a fost data de Doehlert (Fig. 4.15.) care observa ca în procesul de cautare este ignorat punctul cel mai defavorabil. Cautarea optimizarilor se poate face în tot planul, adica în locul unei singure directii de cautare se pot considera N*(N+1) directii de cercetare posibile pentru un singur punct defavorabil. Metoda se numeste "metoda stratului uniform".
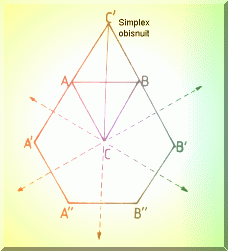
Fig. 4.15. Principiul Doehlert.
4.2.4. Metode de cautare cu evaluarea derivatelor
4.2.4.1. Metoda gradientului (metoda pantei)
Pe baza conditiei minimului functionalei celor mai mici patrate, ![]() din care se determina parametrii
din care se determina parametrii ![]() , observam ca în punctul de minim
putem scrie:
, observam ca în punctul de minim
putem scrie:
![]()
În vecinatatea acestui punct de minim se observa o scadere a valorii gradientului. Un proces iterativ care conduce la scaderea valorii gradientului este:
![]()
unde este un scalar, acelasi pentru toate directiile (Fig.4.16).
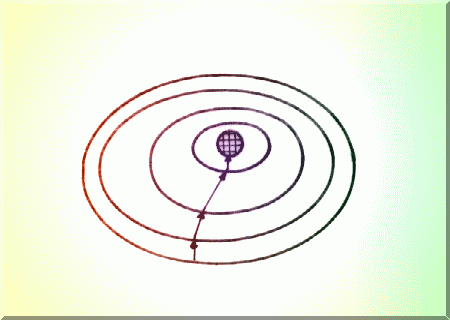
Fig. 4.16. Cautarea prin metoda pantei celei mai accentuate (metoda gradientului).
Dezvoltam functia F în serie Taylor în jurul lui ![]() si avem:
si avem:
![]()
Observam ca ![]() este vector,
este vector, ![]() este un vector si deci al doilea
termen ar putea fi scris ca un produs scalar, astfel încât sa obtinem o scadere a
functiei F prin trecerea de la iteratia k la iteratia k+1. Aceasta alegere este naturala
sub forma:
este un vector si deci al doilea
termen ar putea fi scris ca un produs scalar, astfel încât sa obtinem o scadere a
functiei F prin trecerea de la iteratia k la iteratia k+1. Aceasta alegere este naturala
sub forma:
![]()
si deci:
![]()
iar pentru F avem:
![]()
deci o scadere obligatorie. În aceste relatii k este contorul iteratiilor.
Metoda este foarte populara datorita simplitatii sale.
Etapele algoritmului:
a). Pentru vectorul de pornire ![]() dat, se alege un arbitrar si se determina vectorul
dat, se alege un arbitrar si se determina vectorul
![]()
b).Se calculeaza:
![]()
c). Se testeaza daca:
![]()
Daca da, se continua cu acelasi , în caz contrar se înjumatateste.
d). Se continua iteratiile pâna când noua norma a gradientului este satisfacator de mica sau numarul iteratiilor este prea mare (deci nu am propus niste valori initiale bune), sau s-a obtinut un numar prestabilit de cifre semnificative.
Numarul de cifre semnificative si o norma mica a grdientului înseamna practic ca F = minim cu precizia (grad F)2 si ca metoda este bine aplicata.
Observatie:
metoda gradientului propune acelasi.a pentru toate componentele gradientului. De aceea, este în mod particular ineficient ca una dintre componentele sale sa fie disproportionat de mare fata de celelalte. Acesta conduce la scaderea nejustificata a lui în cursul procesului iterativ. In general, aceasta ajustare este greu de facut si de aceea, pentru valori initiale rau alese scalarul (grad F)2 actioneaza ca o perturbatie asupra lui F care scade pe parcursul procesului iterativ, chiar daca acesta ramâne în principiu convergent.De aceea, pentru cazul test propus, valorile experimentale D(I) sunt împartite la 10.
4.2.4.2. Metoda gradientului conjugat
Aceasta metoda foloseste în plus observatiile legate de simetria suprafetei de
analizat (Fig.4.17.). Se spune ca directiile ![]() si
si ![]() sunt conjugate
daca:
sunt conjugate
daca:
![]()
Fie dezvoltarea în serie a functionalei celor mai mici patrate în forma :
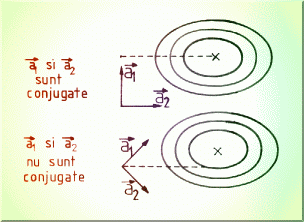
Fig.4.17. Definirea directiilor conjugate.
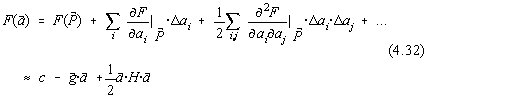
unde:
![]()
![]() este valoarea functionalei celor mai mici patrate în punctul de
pornire
este valoarea functionalei celor mai mici patrate în punctul de
pornire ![]() .
.
![]()
![]() este gradientul functionalei cu semn schimbat în punctul
este gradientul functionalei cu semn schimbat în punctul ![]() , iar
, iar
![]()
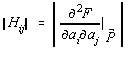
este matricea Hessian asociata functionalei, calculata în punctul ![]() .
.
Sa construim secventa de vectori :
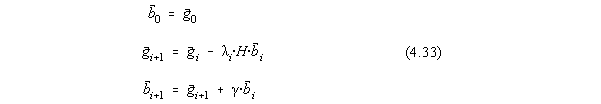
unde i si i sunt alese astfel încât ![]() si
si ![]() , adica :
, adica :
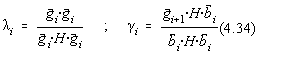
Daca numitorii sunt nuli, i si i se iau 0. Prin aceasta
secventa de calcul, vectorii ![]() sunt
mutual ortogonali iar vectorii
sunt
mutual ortogonali iar vectorii ![]() sunt
mutual conjugati.
sunt
mutual conjugati.
Sa observam ca în apropierea punctului de minim local, putem scrie : ![]() , adica gradientul poate fi obtinut
prin rezolvarea sistemului liniar
, adica gradientul poate fi obtinut
prin rezolvarea sistemului liniar ![]() .
.
Propunem urmatoarea schema de calcul [31] : construim succesiv directii conjugate ![]() pornind de la
pornind de la ![]() si trecem de la
si trecem de la ![]() la
la ![]() dupa directia
dupa directia ![]() catre minimul local al functionalei, unde:
catre minimul local al functionalei, unde:
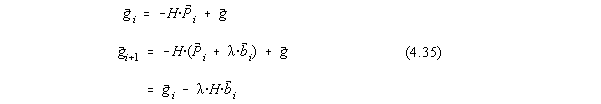
In punctul de minim avem ![]() deci
deci
![]() . De aici rezulta ca :
. De aici rezulta ca :
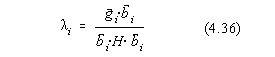
In punctul de minim avem acum simultan ![]() si
si ![]() deci
deci ![]() si atunci prin înlocuirea lui
si atunci prin înlocuirea lui ![]() în expresia lui i obtinem
:
în expresia lui i obtinem
:
![]()
Cautarea se face dupa directiile ![]() , folosind i, fara calculul matricii Hessian.
, folosind i, fara calculul matricii Hessian.
Deoarece aceasta metoda este înrudita cu metoda pantei, observatiile restrictive amintite se aplica si acestei metode (scalarea componentelor gradientului si convergenta lenta daca suntem departe de solutie).
4.2.4.3. Metoda Gauss-Newton pentru functionala celor mai mici patrate
4.2.4.3.1. Principiul metodei
Fie functionala celor mai mici patrate unde M ste numarul punctelor experimentale iar N este numarul parametrilor modelului teoretic. Procedeul Gauss-Newton este iterativ si pentru conciziune notam:
![]()
corectiile parametrului j la iteratia k+1.
Pentru început, dezvoltam în serie Taylor dupa parametrii ai functionala celor mai mici patrate si obtinem la iteratia k [30]:
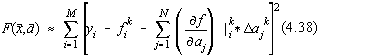
Prin derivarea functionalei (4.23) dupa parametrii aj obtinem:
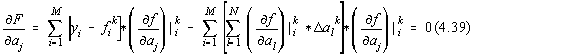
pentru ![]() .
.
Sumele pot fi schimbate între ele obtinându-se :
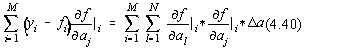
pentru ![]() si care este un
sistem liniar de N ecuatii cu N necunoscute,care mai poate fi scris în forma:
si care este un
sistem liniar de N ecuatii cu N necunoscute,care mai poate fi scris în forma:
![]()
unde :
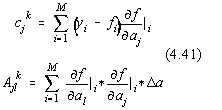
Derivatele partiale pot fi calculate analitic sau numeric în punctul
experimental i la fiecare iteratie, deoarece ![]() este analitica. Calculul numeric al derivatelor partiale se poate efectua
pornind de la formula de definitie:
este analitica. Calculul numeric al derivatelor partiale se poate efectua
pornind de la formula de definitie:
![]()
unde ![]() este ales în
functie de lungimea mantisei calculatorului, de
este ales în
functie de lungimea mantisei calculatorului, de ![]() si de ordinul de marime al parametrului aj:
si de ordinul de marime al parametrului aj:
![]()
4.2.4.3.2. Eroarea în evaluarea parametrilor
Sa consideram ca aproximatie de ordin 0 valorile exacte ale parametrilor. Sistemul liniar:
![]()
ne furnizeaza la sfârsitul procesului iterativ (daca acesta a functionat) chiar
erorile în parametri prin inversa matricii ![]() .
.
Utilizând formal formula lui Kramer pentru solutia sistemului liniar, dispersia pentru parametrul ak are forma:
![]()
unde:
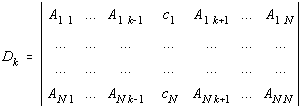
Din formula de propagare a erorilor obtinem:
![]()
respectiv :
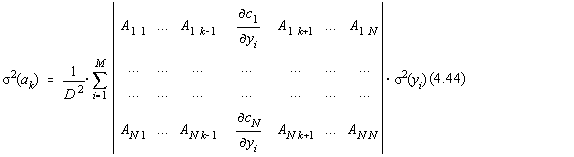
Aceasta expresie poate fi adusa la forma [16]:
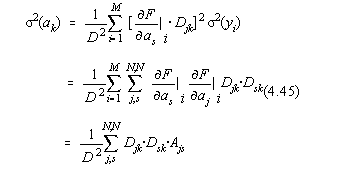
suma care contine dezvoltarea determinantilor dupa linii si care conduce la rezultatul deosebit de simplu de retinut :
![]()
4.2.4.3.3. Algoritmul Levenberg-Marquart
Algoritmul Levenberg-Marquart se bazeaza pe o strategie diferita a pasului, de forma:
![]()
unde: A - matricea derivatelor secunde (Hessianul), iar ![]() - gradientul.
- gradientul.
Practic, matricii sistemului liniar din metoda Gauss-Newton i se adauga pe
diagonala un numar pozitiv mare, l , care are rolul de a
îmbunatati numarul de conditionare al matricii sistemului, care devine astfel dominant
diagonala. Daca pe parcursul procesului iterativ obtinem convergenta, l
este micsorat si la un moment dat, ![]() cu x dat, astfel ca arbitraritatea initiala a
procedeului este îndepartata. Parametrul l trebuie ales astfel
încât la iteratia (k+1), F sa fie mai mic decât la iteratia k. Aceasta conditie este
întotdeauna valabila pentru un l suficient de mare.
cu x dat, astfel ca arbitraritatea initiala a
procedeului este îndepartata. Parametrul l trebuie ales astfel
încât la iteratia (k+1), F sa fie mai mic decât la iteratia k. Aceasta conditie este
întotdeauna valabila pentru un l suficient de mare.
Programul este cu putin mai lent, prin faptul ca valoarea corectiilor este în mod voit mai mica, însa convergenta sa este mult mai buna.
Metoda este recomandata daca gradientul este perpendicular pe directia de cautare, caz în care metoda GaussNewton diverge sau converge încet sau pentru valori initiale ale parametrilor foarte rau alese.