In diapozitivele de mai jos aratam ca metode numerice de baza erau invatate la Bucuresti la sfarsitul sec. XIX
2.1. REZOLVAREA SISTEMELOR DE ECUATII LINIARE
2.1.1. Metoda eliminarii Gaussiene
Metoda lui Gauss este una din cele mai populare metode în rezolvarea sistemelor de ecuatii liniare, calculul determinantilor si determinarea inversei matricilor. Aceasta metoda foloseste algoritmul eliminarii succesive a necunoscutelor, transformând matricea sistemului initial într-o matrice superior triunghiulara.
![]()
2.1.1.1. Rezolvarea sistemelor de ecuatii liniare si calculul determinantilor
Fie un sistem de ecuatii de forma:
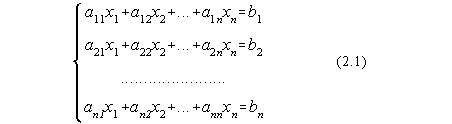
sau scris matriceal sub forma:
![]()
unde:
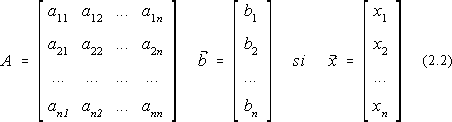
Folosind metoda eliminarii a lui Gauss urmarim sa aducem sistemul de ecuatii (2.1) la forma echivalenta:
![]()
unde:
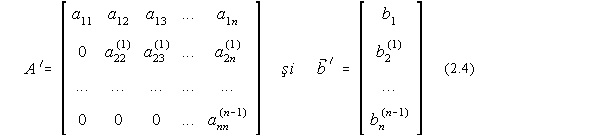
Determinarea elementelor matricilor A' si ![]() se face prin eliminarea succesiva a
necunoscutelor sistemului initial, cu ajutorul relatiilor:
se face prin eliminarea succesiva a
necunoscutelor sistemului initial, cu ajutorul relatiilor:
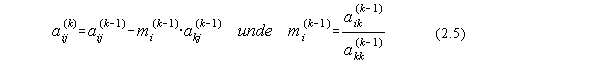
respectiv:
![]()
Solutiile sistemului initial se obtin pe calea substitutiei inverse, cu relatiile:
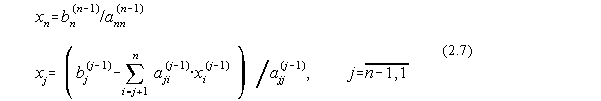
Valoarea determinantului unei matrici superior triunghiulare de forma matricii A' se obtine simplu cu ajutorul relatiei:
![]()
Pentru a putea folosi aceasta metoda este necesar ca elementele generatoare (![]() ) sa nu fie nule. In plus, pot
aparea erori numerice daca elementele generatoare au valori prea mici. Pentru a evita
aceasta situatie se pot inversa ecuatiile sistemului între ele, fapt care duce însa la
schimbarea semnului determinantului. Operatia de permutare a liniilor se numeste pivotare.
Linia de pivotare este linia l corespunzatoare celui mai mare element din coloana
k, adica elementul pivot va fi alk=max(aik),
) sa nu fie nule. In plus, pot
aparea erori numerice daca elementele generatoare au valori prea mici. Pentru a evita
aceasta situatie se pot inversa ecuatiile sistemului între ele, fapt care duce însa la
schimbarea semnului determinantului. Operatia de permutare a liniilor se numeste pivotare.
Linia de pivotare este linia l corespunzatoare celui mai mare element din coloana
k, adica elementul pivot va fi alk=max(aik), ![]() .
.
Daca eliminarea Gaussiana este folosita pentru determinarea inversei unei matrici, atunci este economicos ca detaliile transformarii matricii A, date de o relatie de tipul (2.5) sa fie stocate sub diagonala, astfel încât la eliminarea kpentru linia i vom avea:
T=A(i,k)=A(i,k)/A(k,k)
iar ulterior pentru coloana j:
A(i,j)=A(i,j)-TA(k,j)
In plus, daca au aparut permutari de linii, permutarea trebuie memorata într-un vector întreg:
IP(k)=k
care la permutarea liniilor l si k devine:
IP(k)=l
IP(l)=k
![]()
2.1.1.2. Inversa unei matrici
Fie matricea patrata:
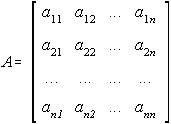
Pentru a gasi inversa acestei matrici se utilizeaza relatia:
AA-1=I (2.9)
unde I este matricea unitate.
Daca matricea inversa A-1 este:
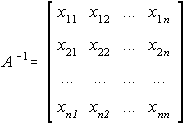
atunci pe baza relatiei (2.8) obtinem:
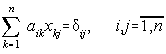
unde d ij este simbolul lui Kronecker.
Cele n sisteme de ecuatii obtinute pentru ![]() au aceeasi matrice A. Numai termenii constanti sunt diferiti si
problema pate fi rezolvata prin metoda lui Gauss pentru a se gasi cele n2
elemente ale matricii A-1.
au aceeasi matrice A. Numai termenii constanti sunt diferiti si
problema pate fi rezolvata prin metoda lui Gauss pentru a se gasi cele n2
elemente ale matricii A-1.
2.1.2. Schema Khaletski (factorizarea LU)
Sa presupunem ca sistemul de ecuatii care trebuie rezolvat este scris sub forma:
![]()
unde matricile A, ![]() si
si
![]() sunt date de (2.2).
sunt date de (2.2).
Dupa cum este cunoscut, cu ajutorul metodei Gauss, solutiile sistemului de ecuatii se obtin simplu daca matricea sistemului este adusa la o forma triunghiulara. Pornind de la aceasta observatie vom scrie matricea sistemului sub forma unui produs de doua matrici L=[lij] si U=[uij], prima inferior triunghiulara, iar cea de-a doua superior triunghiulara cu toate elementele de pe prima diagonala egale cu unitatea:
A=LU (2.11)
unde:
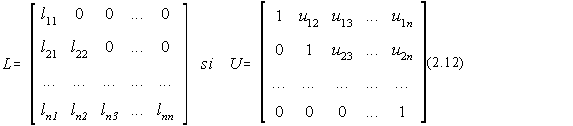
Sistemul initial se scrie acum sub forma:
![]()
![]()
Daca notam ![]() , atunci
rezolvarea sistemului precedent se reduce la rezolvarea urmatoarelor doua sisteme:
, atunci
rezolvarea sistemului precedent se reduce la rezolvarea urmatoarelor doua sisteme:
![]()
cu avantajul ca matricile acestor sisteme sunt matrici triunghiulare.
Mai întâi trebuie rezolvat sistemul (2.14) pentru a se determina solutiile![]() , iar apoi sistemul (2.13) pentru
a se obtine solutiile finale
, iar apoi sistemul (2.13) pentru
a se obtine solutiile finale ![]() .
Desigur ca în prealabil trebuie determinate elementele matricilor L si U. In acest scop,
din egalitatea (2.11) se obtin urmatoarele relatii de recurenta:
.
Desigur ca în prealabil trebuie determinate elementele matricilor L si U. In acest scop,
din egalitatea (2.11) se obtin urmatoarele relatii de recurenta:
![]()
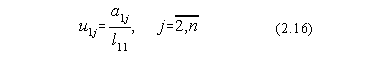
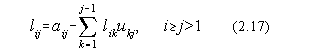
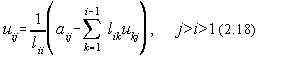
Cunoscându-se elementele matricii L, cu ajutorul ecuatiei (2.14) se obtin solutiile yi:
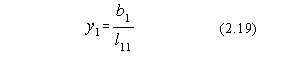
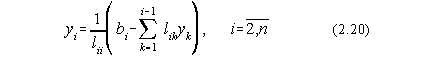
Cunoscând elementele yi si cu ajutorul ecuatiei (2.13) se obtin în final solutiile sistemului initial:
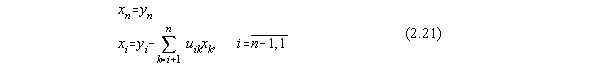
Daca matricea A este simetrica, atunci:
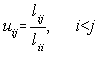
Matricea A va fi folosita pentru memorarea matricilor L si U, iar
vectorul![]() pentru memorarea
vectorilor
pentru memorarea
vectorilor ![]() sau
sau ![]() , dupa necesitati.
, dupa necesitati.
2.1.3. Metoda radacinii patrate (factorizarea TTT) pentru matrici simetrice
Fie sistemul liniar simetric:
![]()
Urmarim sa factorizam matricea A sub forma particulara pentru matrici simetrice:
A=TTT
unde:
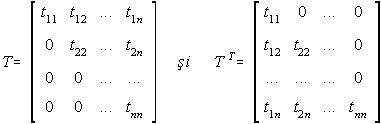
Solutiile sistemului initial se pot obtine prin rezolvarea a doua sisteme de ecuatii a caror matrici sunt T si respectiv TT:
![]()
si ale caror elemente se determina cu relatiile:
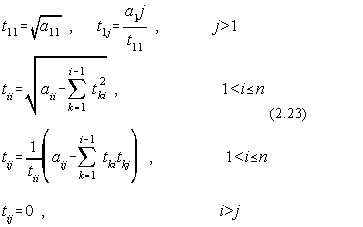
Construirea solutiilor sistemului se face pe baza relatiilor:
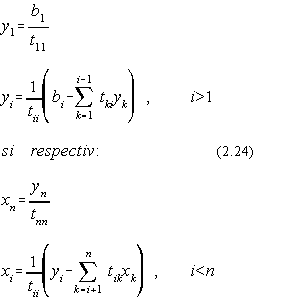
Pentru aceasta metoda, matricea A este stocata sub forma unui vector de
dimensiune n(n+1)/2 care poate fi utilizat si pentru stocarea elementelor tij,
vectorii ![]() si apoi
si apoi ![]() putând fi stocati în vectorul
putând fi stocati în vectorul ![]() . Se obtine astfel o economie
maxima de memorie la rezolvarea sistemelor liniare simetrice.
. Se obtine astfel o economie
maxima de memorie la rezolvarea sistemelor liniare simetrice.
2.2. INTEGRAREA NUMERICA
2.2.1. Interpolarea Lagrange si formula lui Simpson
Fie un set de valori yi coprespunzatoare unui set de puncte discrete xi aflate într-un interval [a,b]. Nefiind cunoscuta forma analitica a functiei y=f(x) se pune problema determinarii unei functii, numita functie de interpolare, ale carei valori în punctele xi (punctele de interpolare) sa fie tocmai valorile corespunzatoare yi. Din punct de vedere geometric problema consta în gasirea curbei y=F(x) care sa treaca neaparat prin punctele (xi,yi) date.
Daca sunt date n+1 puncte de interpolare (x0, x1,...,xn), atunci functia de interpolare trebuie cautata sub forma unui polinom de grad n (polinomul de interpolare Lagrange), Ln(x), cu conditia:
Ln(xi)=yi i=0,1,...,n (2.25)
In scopul determinarii polinomului Lagrange se construieste un polinom pi(x), cu conditia:
![]()
Deoarece acest polinom se anuleaza în n puncte el va avea forma:
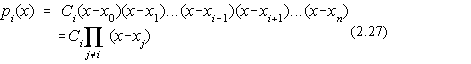
Cum pi(xi)=1, se obtine:
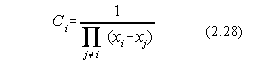
si deci:
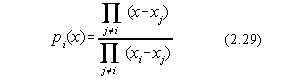
Polinomul Lagrange care satisface conditia (2.25) este:
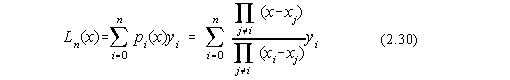
cu conditia:
Ln(xj)=yj
Polinomul de interpolare Lagrange poate fi folosit în locul unei functii tabelate y(xi)
în scopul evaluarii numerice a integralei functiei respective. Daca distanta dintre
punctele de interpolare xi este constanta, atunci pasul de integrare va fi h=xi-xi-1,
iar numarul de intervale pâna la un punct oarecare x este: q=(x-x0)/h.
Cu aceste notatii, polinomul Lagrange poate fi scris:
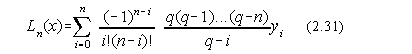
Daca n=2, atunci coeficientii Cotes sunt [6]:
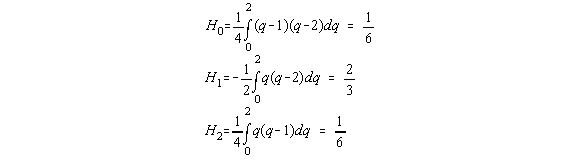
si tinând cont ca x2-x0=2h se obtine formula lui Simpson pentru acest caz simplu (n=2):
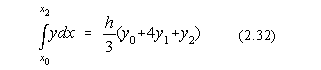
Fie acum un numar par de puncte (n=2m) echidistante. Aplicând formula lui Simpson fiecarui subinterval dublu (x0,x2), (x2,x4),...,(x2m-2,x2m), se obtine formula lui Simpson generalizata:
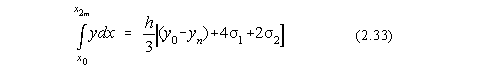
unde:
s 1=y1+y3+...+y2m-1
s 2=y2+y4+...+y2m (2.34)
Eroarea în evaluarea integralei poate fi aflata simplu prin repetarea procedeului pentru un pas înjumatatit, cu formula:
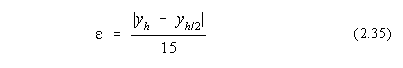
2.2.2. Evaluarea integralelor improprii
Integralele improprii contin functii care [31]:
![]() nu pot fi
evaluate la una din limitele de integrare,
nu pot fi
evaluate la una din limitele de integrare,
![]() au o
singularitete la una din limite, de exemplu
au o
singularitete la una din limite, de exemplu ![]() pentru x=0,
pentru x=0,
![]() au o
singularitate undeva în intervalul de integrare, sau
au o
singularitate undeva în intervalul de integrare, sau
![]() limitele de
integrare sunt +Ľ sau -Ľ
limitele de
integrare sunt +Ľ sau -Ľ
Una dintre solutiile cele mai simple consta în schimbarea de variabila t=1/x, adica:
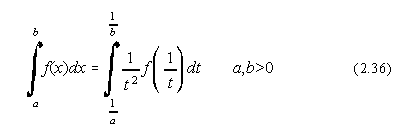
Pentru integralele care au o singularitate de tip putere la limita inferioara,
adica (x - a), 0 1, pentru x=0, putem folosi:
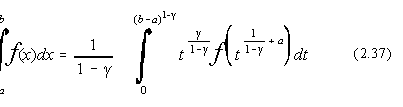
Pentru singularitatile frecvente de tip inversul radacinii patrate folosim:
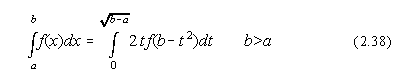
Pentru cazul limitelor de integrare de tip putem folosi substitutia x=-lnt:
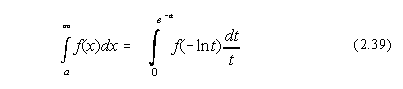
![]()
Pentru integralele improprii convergente, fara singularitati, putem formula un procedeu general bazat pe utilizarea preciziei sistemului de calcul. Deoarece integrala este o suma, ultima valoare calculata a functiei care nu mai modifica valoarea sumei este data de variabila REPS din capitolul I. Folosind metoda lui Newton pentru ecuatia neliniara f(x)-REPS=0 aflam valoarea abscisei pentru care putem închia integrarea. Apoi, aplicam formula lui Simpson pentru calculul integralei între limitele de integrare care au astfel valori bine determinate. Numarul de pasi poate fi eventual ajustat tinând sema de eroarea calculata cu formula (2.35).
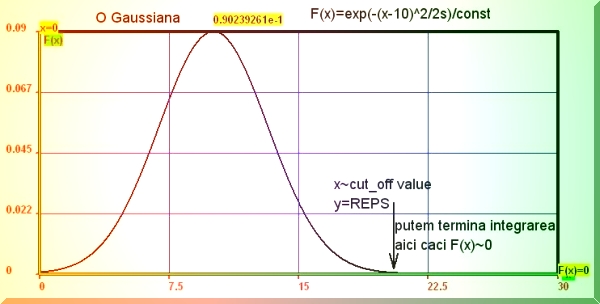
2.2.3. Integrale multiple. Metoda Monte-Carlo
Valoarea integralelor unidimensionale, poate fi estimata cu ajutorul relatiei (Fig.2.1.):
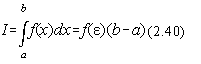
Daca alegem b-a=1, adica daca se transforma intervalul [a,b] în intervalul [0,1], atunci o evaluare a lui f(e ) se poate obtine dupa un numar mare de încercari n:
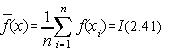
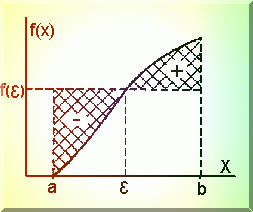
Fig. 2.1. Semnificatia geometrica a teoremei de medie
Generarea valorilor x se poate face folosind generatorul intern de numere aleatoare caracteristic limbajului de programare folosit. Utilizarea numerelor aleatoare este justificata de faptul ca ordinea termenilor din suma (2.48) este indiferenta. Metoda Monte Carlo este utilizata în special pentru calculul comod al integralelor multiple.
Fie cazul test [6]:
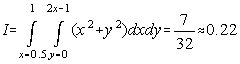
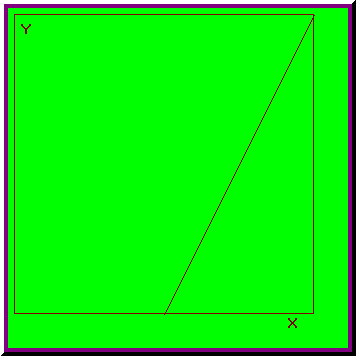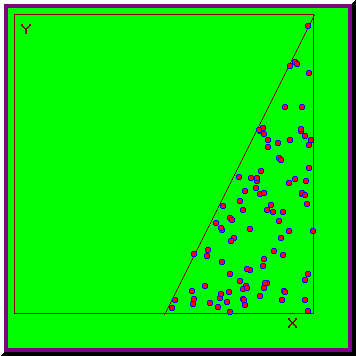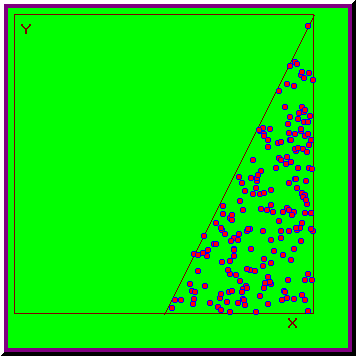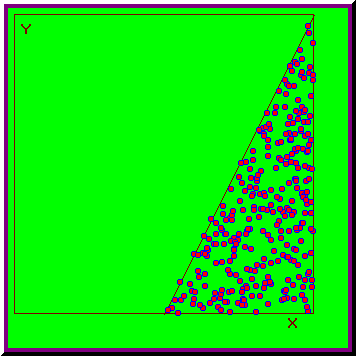
Fig. 2.2. Domeniul de integrare pentru cazul test
Daca generam C numere aleatoare, doar n dintre ele se vor afla în intervalul de definitie, astfel încât:
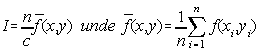
Asadar vom avea:
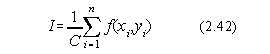
Metoda Monte-Carlo asigura obtinerea unor valori aproximative ale integralelor multiple, foarte apropiate de cele exacte dupa un numar mare de evaluari.
In cazul în care intervalul de definitie al variabilelor de integrare nu este [0,1] se face transformarea de variabila xiyi:
xi=ximinim+(ximaxim-ximinim)*yi pentru 0yi1.
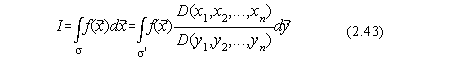
în care:
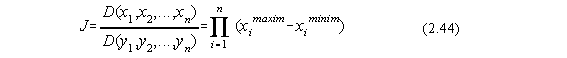
este Jacobianul transformarii.
Daca notam:
![]()
atunci avem:
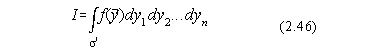
Dispersia si eroarea patratica se determina conform formulelor din Cap.3.
2.3. DERIVAREA NUMERICA
Desi, în principiu, derivarea poate fi efectuata analitic, în cazul functiilor complicate exista riscul unor greseli inerente si în plus în unele programe este necesar un calcul numeric al derivatelor.
Una dintre metodele folosite în derivarea numerica porneste de la folosirea polinomului Lagrange care poate sa treaca prin mai multe puncte echidistante. Fie polinomul de interpolare care trece prin trei puncte echidistante:
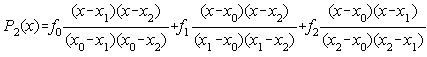
Derivata acestui polinom este:
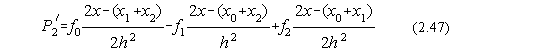
unde:
xj=x0+jh, j=1,2,...,n (2.48)
Tinând cont de ultima relatie, derivatele de ordin 1 si 2 în punctele x0,x1 si respectiv x2 sunt:
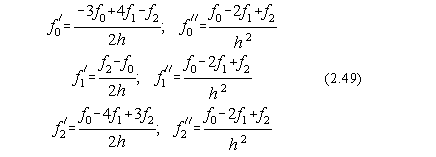
In cazul unui polinom de interpolare care trece prin cinci puncte:
![]()
Evident ca în acest caz, pentru primele si ultimele doua puncte, derivata trebuie calculata cu formulele anterioare (2.56).
![]()
O solutie mult mai expeditiva este data de formula de definitie a derivatei partiale:
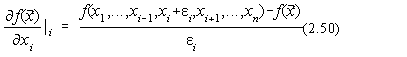
Alegerea lui trebuie facuta cu atentie deoarece un e prea mic duce la fluctuatii false ale derivatei. De asemenea o valoare prea mare a lui e implica o evaluare prea grosiera a derivatei numerice.
O solutie care da rezultate bune în majoritatea cazurilor consta în considerarea
lungimii mantisei calculatorului. Pentru valori ale functiei f(x) de ordinul unitatii, o
valoare potrivita pentru pasul derivatei, e , este jumatate din lungimea mantisei, ![]() .
.
Pe de alta parte trebuie sa se tina cont si de ordinul de marime al variabilei xi. In acest caz se va folosi functia: e i=EPS* MAX(ABS(xi),0.1), în care valoarea 0.1 este luata ca referinta deoarece de la aceasta valoare calculatorul trece la reprezentarea numerelor în virgula flotanta (mobila).
2.4. METODA LUI NEWTON PENTRU REZOLVAREA ECUATIILOR SI SISTEMELOR DE ECUATII NELINIARE
Pentru ecuatiile neliniare, metoda lui Newton foloseste procesul iterativ:
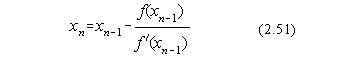
dedus din dezvoltarea în serie Taylor a functiei f(x).
Fie cazul test: f(x)=x4+2x3-x-1 cu radacina 0.867.
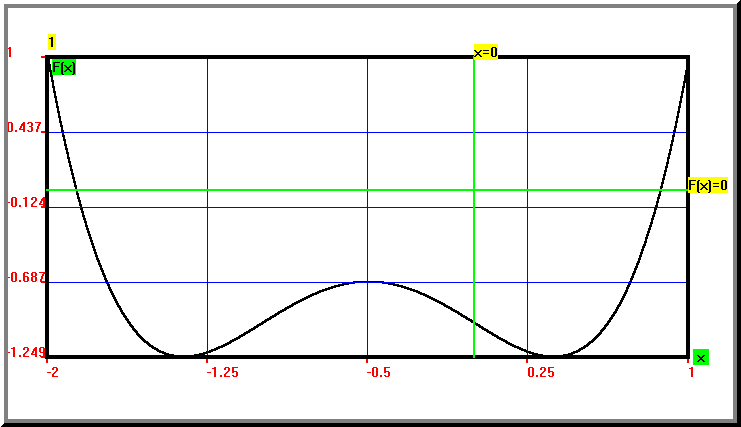
Metoda descrisa mai sus pentru rezolvarea unei ecuatii neliniare poate fi generalizata pentru un sistem de ecuatii neliniare. Fie pentru început un sistem de doua ecuatii neliniare cu doua necunoscute:
f(x,y)=x3-3xy2-2x+2=0
g(x,y)=3x2y-y3-2y=0 (2.52)
cu solutiile: x=0.884646 si y=0.589743.
Dezvoltam în serie Taylor cele doua functii f si g:
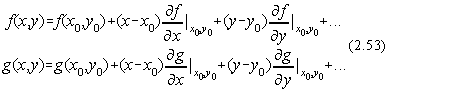
Daca ne oprim la primii doi termeni ai dezvoltarii obtinem urmatorul proces iterativ:
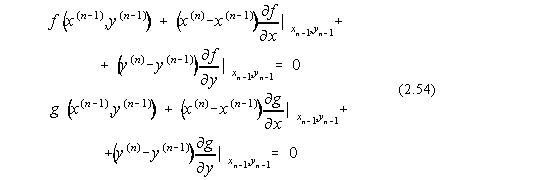
La fiecare iteratie se vor actualiza valorile xn-1 si yn-1. Pentru cazul test calculul se continua pâna la precizia calculatorului.
Programele exemplificative folosesc o procedura mai generala, utilizând derivarea numerica.
Pentru un numar oarecare de ecuatii, sistemul neliniar se pune sub forma:
![]()
In acest caz, pentru sistemul liniar utilizat iterativ în metoda lui Newton se obtine:
![]()
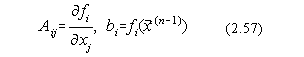
unde ![]() se numesc
corectii ale solutiei, iar procesul iterativ se scrie sub forma:
se numesc
corectii ale solutiei, iar procesul iterativ se scrie sub forma:
![]()
sau scalar:
![]()
Metoda lui Newton modificata se bazeaza pe observatia lui Kantorovici ca matricea A-1 se modifica putin în vecinatatea solutiei si de aceea poate fi folosita la mai multe iteratii.
2.5. METODA RUNGE-KUTTA PENTRU REZOLVAREA ECUATIILOR SI SISTEMELOR DE ECUATII DIFERENTIALE ORDINARE
Ecuatiile diferentiale descriu fenomene tranzitorii, cum ar fi încarcarea unui condensator sau ecuatia lui Schrödinger unidimensionala dependenta de timp.
Cel mai simplu caz, al fenomenelor care depind de o singura variabila, are forma:
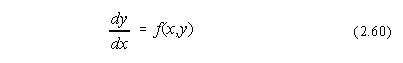
cu conditia initiala (la limita) y(x0)=a,unde x0 si a sunt constante, provenite, de exemplu, din masuratori experimentale.
Ecuatia diferentiala este folosita pentru a afla valoarea lui y pentru un x diferit de x0. Deci rezolvarea (integrarea) ecuatiei diferentiale este o metoda de extrapolare.
Cea mai simpla abordare este metoda lui Euler, sau a liniilor poligonale, care foloseste din nou dezvoltarea în serie a functiei y:
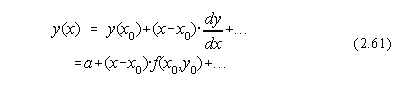
Aceasta relatie permite aproximarea functiei în punctul x din aproape în aproape prin alegerea judicioasa a unui pas, h=x-x0 suficient de mic.
O aproximare mult mai buna este data de metodele Runge-Kutta, în care se foloseste observatia ca dezvoltarea în serie Taylor produce un polinom de aproximare al functiei, iar derivatele de ordin superior pot fi calculate pornind de la f(x,y). Dupa numarul de termeni din dezvoltare, sunt descrise metodele Runge-Kutta de ordinele I, II, III, IV si V.
Sa scriem noua aproximatie a lui y în forma:
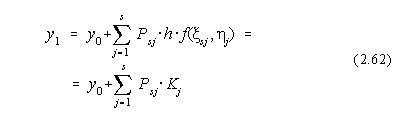
unde variabilele si desemneaza vecinatatea lui x respectiv y fata de care se face aproximarea. In aceasta formula impunem conditia ca dezvoltarea în serie dupa puterile lui h sa coincida cu dezvoltarea în serie a functiei exacte y(x), pentru o putere cât mai mare, s.
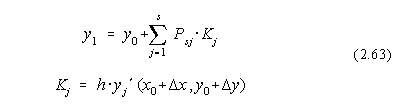
unde
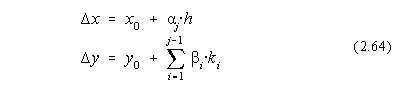
Fie s=1 si atunci
![]()
Deci, metoda lui Euler este echivalenta cu metoda Runge-Kutta de ordinul I. Functia trebuie calculata o singura data la fiecare crestere a variabilei cu h.
Fie s=2. Dezvoltarea în serie Taylor are forma:
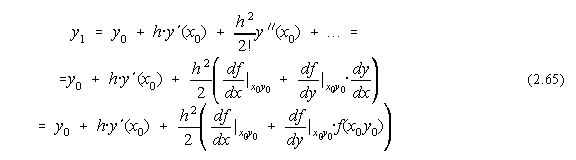
Cu notatiile Runge-Kutta avem:
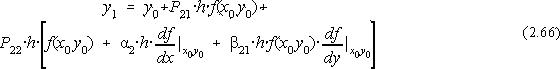
Identificând termenii dupa puterile lui h obtinem:
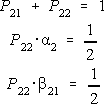
Se alege P22=1/2 si atunci P21=1/2, a 2=1, b 21=1. Rezulta:
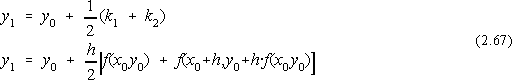
La fiecare etapa de calcul, functia trebuie evaluata de doua ori.
![]()
Cea mai populara metoda este insa metoda Runge-Kutta de ordinul IV pentru care mnemonica este deosebit de simpla prin memorarea secventei "1221".
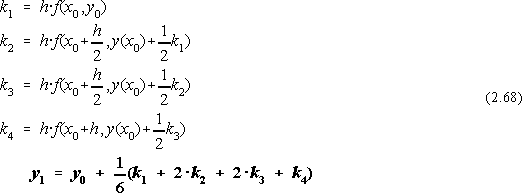
Pentru alegerea judicioasa a pasului se verifica marimea:
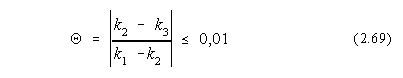
Eroarea poate fi evaluata de asemenea prin repetarea calculului pentru un pas înjumatatit:
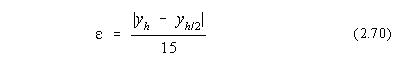
Generalizarea pentru sisteme de ecuatii diferentiale ordinare se obtine simplu. Fie cazul unui sistem de doua ecuatii diferentiale ordinare:
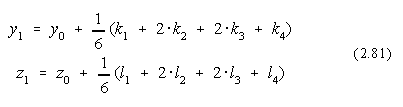
unde:
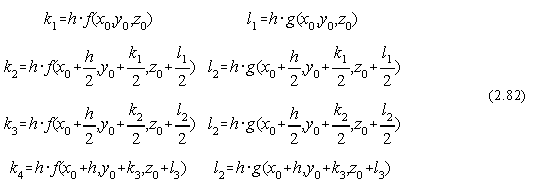
Pentru rezolvarea ecuatiei lui Scrödinger unidimensionale, observam ca o ecuatie diferentiala de ordinul doi se reduce la un sistem de ecuatii diferentiale ordinare prin substitutia
y1(x)=y(x)
si respectiv
y2(x)=y(x).
Ecuatia lui Scroedinger, unidimensionala, dependenta de timp are forma:
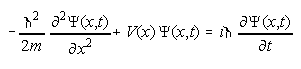
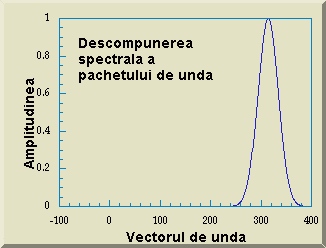
Pachetul de unde, care reprezinta solutia, se ia în forma functionala:
![]()
care consta din produsul unei unde plane cu o Gaussiana. Probabilitatea de a localiza particula cuantica, produsul y y *, este o Gaussian pura.
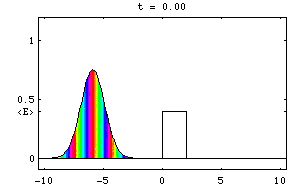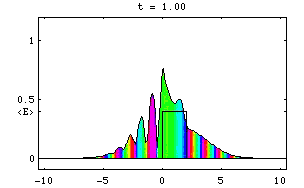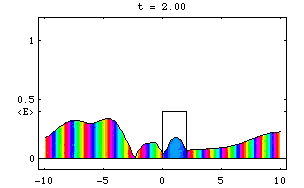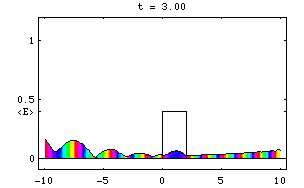
Pentru partea reala a funciei de unda avem reprezentarea grafica urmatoare:
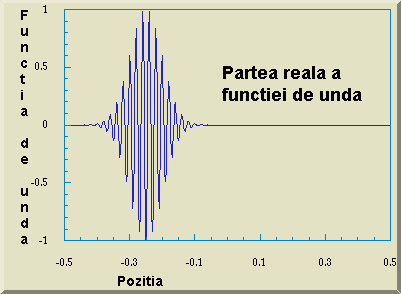
Functia de unda se normeaza la unitate în modul cunoscut,
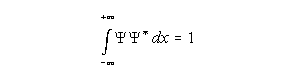
Pachetul de unde a fost astfel ales pentru a prezenta localizarea asteptata a unei particule în spatiu. Trebuie însa sa observam ca ecuatiile diferentiale admit întotdeauna o suprapunere de solutii, pe care le putem scrie în forma unei suprapuneri de armonici:
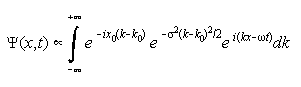
Prima exponeniala ne da faza, iar a doua, dependenta de s, ne da impresia de puritate spectrala. Pachetul de unde este o suprapunere de unde plane cu vectori de unda k apropiati. Amplitudinea functiei este maxima in jurul lui k0, dar vom obtine o alterare importanta a acestui aspect la o interactiune.
De aceea, pentru reprezentarea fazei se imprumuta compozitia spectrala a luminii:
Fie acum cazul unei bariere de potential:

Pentru acest caz obtinem urmatoarea reprezentare a undei incidente, reflectate, transmise si a alterarii fazei: